ML Basics: K Nearest Neighbors

One of the things I like about the Google Cloud Developer Advocacy team is that many of us have a similar sense of humor. Last year we had an ongoing joke about what the [D&D](https://en.wikipedia.org/wiki/Alignment_(Dungeons_%26_Dragons) alignment of each team member was based on their behavior at work. For the record, it was decided that I was Chaotic Good which sounds about right in my opinion.

Our D&D alignment game was a form classification. We were putting our co-workers (data points) into categories (classes) based on their attributes. Classification problems, and related clustering problems, are a large percentage of machine learning problems.

One technique for doing classification is called K Nearest Neighbors or KNN. To use the algorithm you need to have some data that you’ve already classified correctly and a new data point that you wish to classify. Then you find the K (a somewhat arbitrary number) of existing data points that are the most similar (or near) to your new datapoint. You assign the new datapoint to whatever class the majority of the neighbors have.

Problem and Dataset

The Iris Flower Dataset has been used to demonstrate classification problems for years. This dataset was originally published in 1936. It records the sepal length and width, the petal length and width, and the species for 50 observed irises. There are three possible species: Iris Setosa, Iris Virginica, and Iris Versicolor.

I hope that by using KNN I’ll be able to predict the species of a new observation using KNN. I’ll find which K observations already in the dataset are most similar to the new observation and then assign the new observation to the same species as a majority of the neighbors.

Similarity and Distance

To define the concept of neighbors I need to have some measure of distance. It is a bit odd to talk about the “distance” between two flowers so you can also think of it as another way of saying similarity.

To understand why it is called distance it is helpful to visualize the data. To start with, here’s a scatterplot of petal length and width.

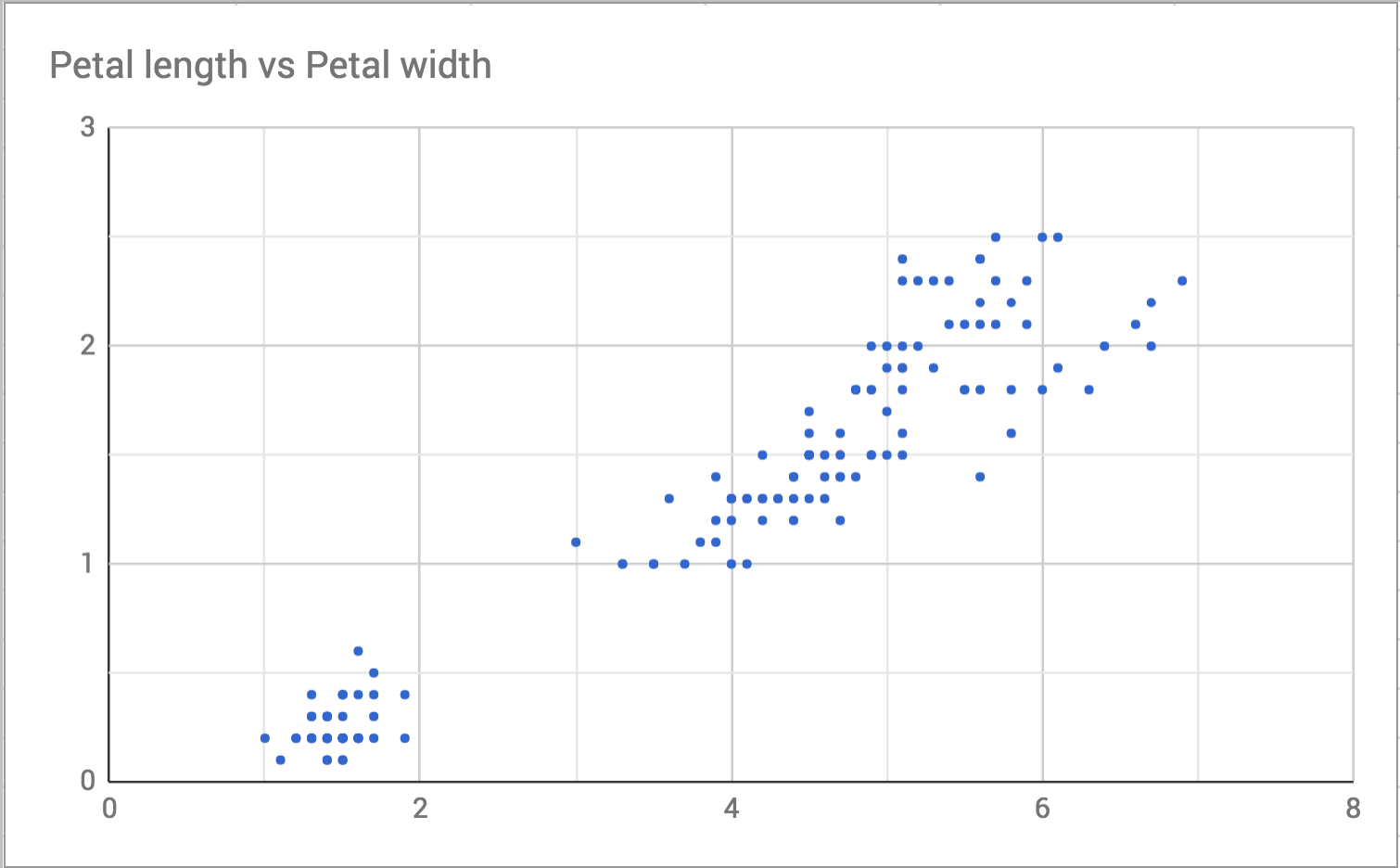
I choose one point in the plot to focus on, like this:

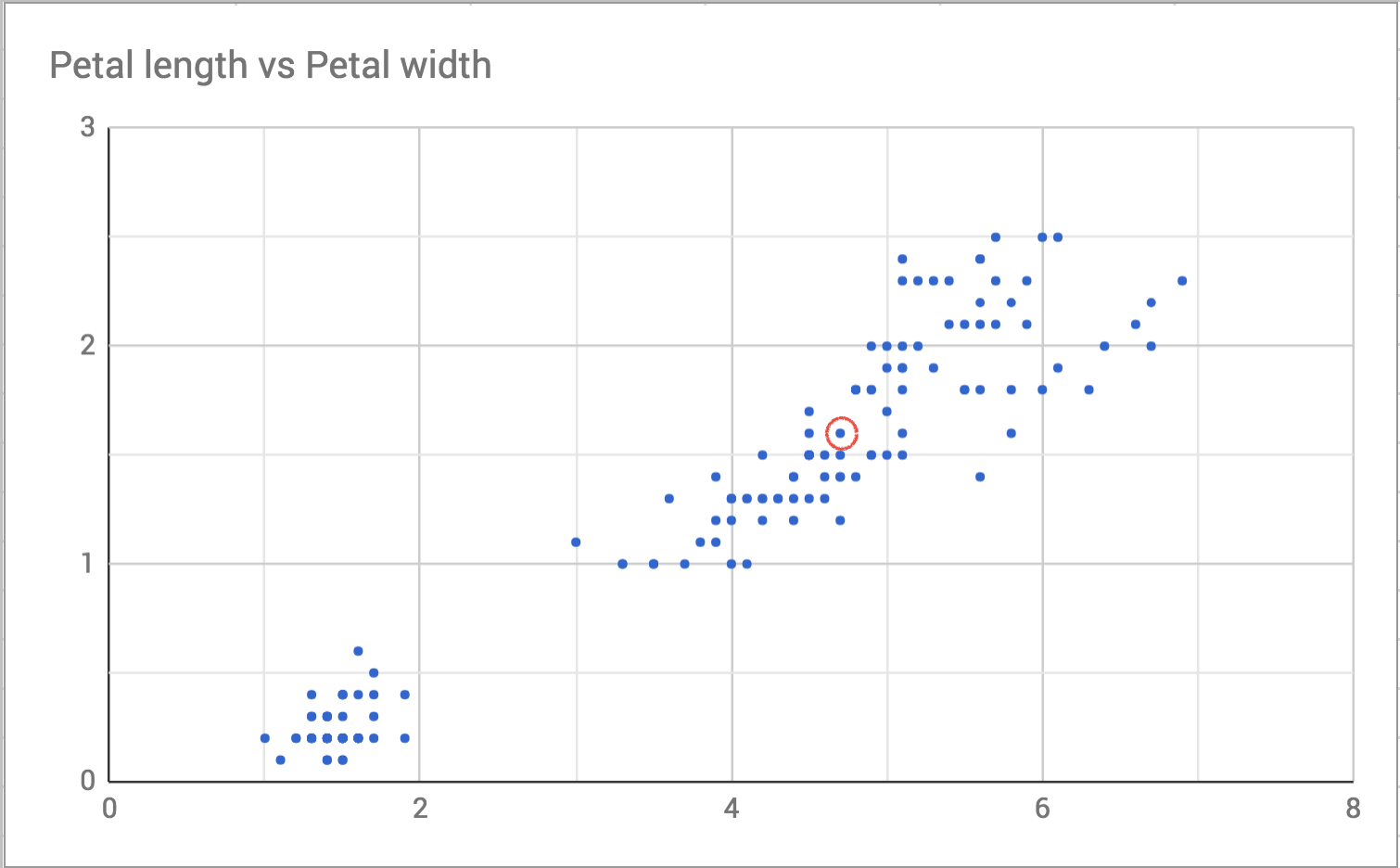
Then I draw a slightly bigger circle around it to see who the neighbors are.

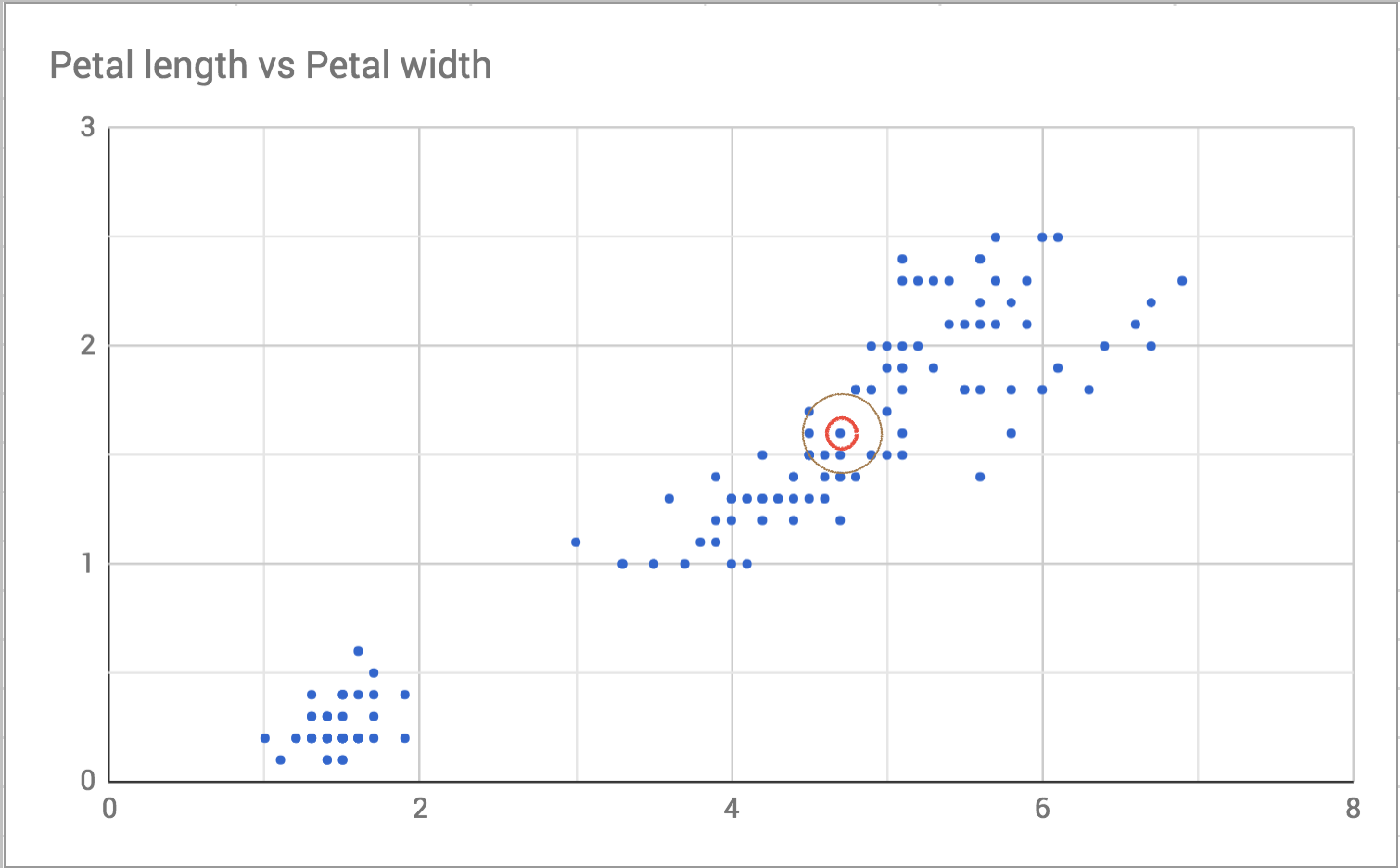
So the neighbors are the points that are closest, or the least distance, away. On an x-y plane like the one in the scatterplot, we can calculate distance using the distance formula from geometry. This formula generalizes to as many dimensions as we need. Here’s an implementation in Ruby using Array#zip and Enumerable#inject. I could have done the whole thing in a single line. That requires using the more complicated version of inject. I think this version is easier to understand even if it is slower.

def distance ary1, ary2
  paired_points = ary1.zip(ary2)

  Math.sqrt(paired_points.map { |a, b| (a - b)**2 }.inject(:+))
end

There are other ways to calculate distance like Manhattan Distance and Chebyshev Distance but regular geometric distance is good enough for this problem.

Detection of K Nearest Neighbors

In large datasets, there are special data structures and algorithms you can use to make finding the nearest neighbors computationally feasible. But this dataset is small enough that I can just iterate over all the data points and sort them by distance. Say I have a new iris, and it has a sepal length of 5.0, a sepal width of 3.0, a petal length of 4.4, and a petal width of 1.6. I want to figure out what species it is likely to be so I look at the three known data points nearest to my new iris and decide my new iris is probably the same species as the majority of its neighbors.

new_iris = [5.0, 3.0, 4.4, 1.6, nil]


data = CSV.read("iris.csv", converters: :all ).to_a

data.shift # Remove the header

neighbors = data.min_by(3) { |ary| distance new_iris[0..3], ary[0..3] }

puts neighbors.group_by { |a| a[4] }.max_by { |k, v| v.count }[0]

This code uses a bunch of Ruby’s enumerable methods that you may not have seen before. I call min_by with a block and an argument. The block calculates the distance between the new iris and the known irises. The argument, 3 in this case, is the number of items I want to return. So that line returns the 3 known irises that are closest (have the minimum distance) to the new iris. I’m calculating the distance with only the numeric parts of the data which is the first four elements in each row. Then, I take the neighbors, group them by the species name (the fifth element in the array), and print whichever species had the most results.

An important note, min_by(n) { |obj| block } was added in Ruby 2.2. Before that, you could only get a single value from the min_by method. That means the code above will not work with the default Ruby on Mac OS, which is Ruby 2.0.0. If you want to run this code in Ruby 2.0.0 you can use sort_by and first like this:

neighbors = data.sort_by { |ary| distance new_iris[0..3], ary[0..3] }.first(3)

puts neighbors.group_by { |a| a[4] }.max_by { |k, v| v.count }[0]

This problem is also a great example of why knowing the methods on collection classes is helpful. I could have written this using iterators like each, but this version is both less error prone and more intention revealing. And these methods are written in C so they’re faster than anything I’d write in pure Ruby.

Selection of K

The code above prints out “I. Versicolor” for my new iris. But I picked three neighbors mostly at random. If I only look at 2 neighbors, I get a tie between “I. Versicolor and I. Verginica. It turns out that you can mostly pick K at random or based on your intuition as long as you follow some basic guidelines.

First, I need to choose a K so that I avoid ties. This data set has 3 species. If I chose 3 (or 6 or 9) for K I might end up with a tie. So I should choose some number that isn’t a multiple of 3.

Second, I need to choose K that isn’t too small. If I choose 2 in the example above I get a tie between I. Versicolor and I. Virginica. But if I choose any number between 3 and 20 it is clear that the majority of neighbors are I. Versicolor. By choosing a small number I may not be seeing the whole picture.

Third, I need to choose K that isn’t too big. If my data set was half I. Versicolor and I choose a large K it would be likely that more neighbors were I. Versicolor just because there were more I. Versicolor data points in the data set. Also, looking at more data points can make the algorithm slower.

For this data set, K = 5 seemed reasonable. It isn’t a multiple of 3. It isn’t so small that the nearest neighbors will bias it and it isn’t so large that it will reflect the underlying data set.

Conclusion

This is just the surface of the K nearest neighbors algorithm. You can use different ways of calculating distance to better model the data you are using. You can also use techniques such as weighting responses by the distance, so closer neighbors count more than neighbors that are a bit further away. This post talks about the K Nearest Neighbors classification algorithm. We have the neighbors “vote” and take the majority response. I used classification here because the value I’m trying to predict is the species (a category/class). If I was trying to predict a numeric value I could instead use a K Nearest Neighbors regression and average the values my neighbors have for a given field.

I like this algorithm because it makes a fair amount of intuitive sense. If you don’t know what value goes in a blank, it makes sense to look at similar items and make your decision from there. I think this makes it a good introduction to machine learning.